administração,11,administração financeira,1,administração orçamentária,1,administração pública,2,ads,39306,advogado,1,agricultura,1,agronomia,8,alberteinstein,27,alfabeto,5,amrigs,3,anasem,1,anatomia,2,aocp,142,arquitetura,1,arquitetura e urbanismo,7,arquivologia,1,arte,10,artes visuais,1,artes visucais,2,assistente social,2,atividade,289,atividade biologia,8,atividade ciências,68,atividade de português,58,atividade espanhol,17,atividade filosofia,5,atividade física,8,atividade fundamental,213,atividade geografia,6,atividade história,84,atividade inglês,2,atividade literatura,3,atividade matemática,27,atividade quimica,7,atividade sociologia,3,auditor fiscal,1,auditoria,1,autoajuda,1,auxiliar administrativo,3,auxiliar judiciário,1,bem-estar,13,biblioteconomia,4,biografia,1,biologia,65,biomedicina,11,bioquimica,1,blogger,3,bncc,12,bolsafamilia,1,braille,1,callfrom,1,carnaval,2,cecierj,5,cederj,5,cefetba,40,cefetmg,35,celebridades,1,celpebras,1,cesgranrio,52,cfc,13,ciência da computação,1,ciencias,85,ciências biológicas,2,ciências contábeis,21,ciências da computação,1,ciências da saúde,1,ciências econômicas,5,ciências sociais,4,claudiogaleno,1,colunas,11,comercio exterior,1,computação,5,comunicação social,1,concurso,507,conhecimento específico,3,conscam,45,conta pra mim,41,contabilidade,13,contabilidade avançada,1,contabilidade de custos,1,contabilidade pública,10,contabilidadedecustos,1,contador,5,coronavirus,8,criminologia,1,cultura,30,curiosidade,5,datas comemorativas,25,declaracoes,6,desenhos,449,design,6,design de interiores,1,design de moda,1,design grafico,1,destaque,12,detran,2,devry,1,dietética,2,direito,160,direito administrativo,36,direito ambiental,2,direito civil,29,direito constitucional,36,direito do trabalho,27,direito eleitoral,1,direito empresarial,28,direito financeiro,1,direito penal,30,direito processual civil,1,direito processual do trabalho,1,direito processual penal,2,direito tributário,34,direitoadministrativo,2,direitocivil,3,direitos humanos,1,duvidas,5,economia,3,educação,55,educação física,20,educação infantil,351,eleicoes,1,enade,412,enamed,1,enare,1,encceja,44,enem,98,enfermagem,21,engenharia,5,engenharia ambiental,4,engenharia civil,5,engenharia da computação,5,engenharia de alimentos,4,engenharia de controle e automação,2,engenharia de produção,4,engenharia eletrica,3,engenharia florestal,3,engenharia mecanica,3,engenharia quimica,3,ensino fundamental,352,escola,1,espanhol,40,espcex,36,especial,1,espm,7,esportes,1,estatística,2,exame nacional,3,explicacao,48,facid,1,faculdade,30,faculdade dinamica,2,fadip,1,fagoc,2,famema,30,famerp,14,farmacia,12,fasa,9,faseh,1,fatec,29,fcc,107,fdsbc,4,fei,19,fgv,32,filosofia,25,fiscal de obras e posturas,1,fisica,66,física,1,fisioterapia,11,fmabc,5,fmo,2,fonoaudiologia,10,formação geral,9,formula1,1,fps,35,frances,7,frases,1,fuvest,24,gabaritos,35,gastronomia,3,geografia,77,gestao ambiental,3,gestão comercial,3,gestão da qualidade,1,gestao de qualidade,1,gestao de recursos humanos,3,gestão de recursos humanos,1,gestão financeira,4,gestao hospitalar,4,gestão pública,2,habilidades bncc,76,historia,177,ibade,5,ifba,1,ifce,12,iff,1,ifmg,3,ifmt,135,ifnmg,1,ifpe,66,ifpi,12,ifsul,67,ifto,12,imagens,96,ime,68,informatica,11,inglês,60,insper,52,instituto acesso,138,ita,22,jornalismo,16,legislação,10,legislação penal,1,legislação tributária municipal,13,leituras,1,lendas,23,letras,2,libras,2,liceu piauiense,1,literatura,23,livros,1,lixo,12,logística,2,loja,3,mackenzie,28,marketing,3,matematica,123,matemática financeira,1,medicina,96,medicina legal,2,medicina veterinaria,11,meliuz,1,mtc,1,musica,4,música,1,natal,2,necropsia,1,normal superior,1,noticias,117,nubank,4,nutrição,15,o que e,3,oab,215,obmep,10,odontologia,12,outros,75,pedagogia,7,piaui,1,pnaic,10,portugues,161,praticapsi,14,priuni,1,processos gerenciais,4,procurador,2,professor,18,pronatec,3,prouni,5,prova da cebraspe,1,prova da ebserh,1,prova de enfermagem,1,provas,1475,provas access,1,provas agirh,8,provas albert einstein,10,provas ameosc,2,provas amrigs,3,provas avança sp,5,provas cecierj,2,provas cefetmg,35,provas cfc,13,provas cnu,9,provas concurso,305,provas da univesp,2,provas enade,411,provas enamed,1,provas enare,1,provas encceja,35,provas enem,38,provas espcex,11,provas espm,4,provas famema,17,provas famerp,10,provas faseh,1,provas fatec,23,provas fdsbc,2,provas fei,2,provas fepese,17,provas fgv,13,provas fmabc,3,provas fmj,2,provas fmp,1,provas fundatec,5,provas fuvest,14,provas iades,2,provas ibest,1,provas ibfc,7,provas ieses,3,provas ifba,1,provas ifce,2,provas ifmg,3,provas ifmt,1,provas ifnmg,1,provas ifpi,13,provas ifsul,9,provas ifto,8,provas ime,1,provas ita,12,provas mackenzie,18,provas mestrado,1,provas mpe-go,1,provas nível fundamental,3,provas nível médio,26,provas nível superior,158,provas oab,216,provas puc,9,provas pucgo,2,provas pucrj,4,provas quadrix,2,provas reis&reis,1,provas residencia,51,provas revalida,12,provas santa casa,9,provas ucpel,2,provas uece,16,provas ueg,8,provas uel,5,provas uem,3,provas uema,5,provas uenp,1,provas uepg,1,provas uerj,2,provas uesb,1,provas ufac,5,provas ufgd,9,provas ufpel,1,provas ufpr,1,provas ufrgs,1,provas ufu,1,provas unemat,1,provas unesc,7,provas unesp,9,provas unicamp,12,provas unicentro,1,provas unicesumar,7,provas uniceub,2,provas unichristus,5,provas unifenas,6,provas unifesp,22,provas unifor,7,provas unioeste,3,provas unip,3,provas unirg,9,provas unirv,3,provas unisc,2,provas unitins,4,provas upe,17,provas uri,1,provas usp,52,provas vestibular,471,provas vunesp,2,psicologia,38,publicidade e propaganda,4,publieditorial,2,puc-go,4,puc-pr,2,puc-rs,106,puc-sp,69,pucrj,1,questão agirh,34,questão alemao,8,questão análise e desenvolvimento de sistemas,25,questão analista em tecnologia da informação,30,questão anasem,60,questão arquitetura e urbanismo,176,questão atualidades,50,questão automação industrial,26,questão auxiliar judiciário,48,questão avmoreira,59,questão cecierj,64,questão cederj,128,questão cespe,221,questão cnu,40,questão comercio exterior,54,questão computação,136,questão comunicação social,24,questão construção de edifícios,27,questão consulplan,20,questão consultor do tesouro estadual,39,questão coronavirus,25,questão cremern,27,questão crespe,659,questão da access,40,questão da agirh,60,questão da albert einstein,557,questão da ameosc,40,questão da amrigs,181,questão da aocp,50,questão da avança sp,110,questão da cebraspe,120,questão da cesgranrio,282,questão da espcex,796,questão da espm,80,questão da famema,521,questão da famerp,230,questão da fasa,102,questão da fatec,1307,questão da fau,96,questão da fcc,460,questão da fepese,489,questão da fgv,2891,questão da fmabc,170,questão da fmp,60,questão da fundatec,60,questão da fuvest,1255,questão da mpe-go,50,questão da oab,3663,questão da obmep,326,questão da puc-pr,103,questão da puc-rj,81,questão da puc-sp,243,questão da santa casa,581,questão da ucpel,64,questão da uece,1134,questão da ueg,380,questão da uel,453,questão da uema,352,questão da uemg,115,questão da uenp,65,questão da uerj,140,questão da ufac,209,questão da ufgd,476,questão da ufpel,106,questão da ufrgs,25,questão da unesc,68,questão da unesp,1061,questão da unicamp,884,questão da unicentro,256,questão da unicesumar,223,questão da uniceub,108,questão da unichristus,381,questão da unifenas,299,questão da unifesp,900,questão da unifor,453,questão da unioeste,164,questão da unip,149,questão da unirg,473,questão da unirv,181,questão da unisc,88,questão da unitins,209,questão da usp,1304,questão da vunesp,60,questão de administração,249,questão de administração financeira,6,questão de administração financeira e orçamentária,7,questão de administração orçamentária,6,questão de administração pública,96,questão de agronomia,179,questão de análise das demonstrações contábeis,2,questão de análise de dados,17,questão de anatomia,20,questão de arte,70,questão de artes,83,questão de artes visuais,82,questão de auditoria,25,questão de auditoria governamental,7,questão de biblioteconomia,39,questão de biologia,1652,questão de biomedicina,269,questão de braille,10,questão de ciências,765,questão de ciências biológicas,111,questão de ciências contábeis,196,questão de ciências da computação,171,questão de ciências da saúde,20,questão de ciências econômicas,200,questão de ciências humanas,219,questão de ciências naturais,249,questão de ciências sociais,123,questão de cirurgia cardiovascular,30,questão de código de defesa do consumidor,10,questão de computação,57,questão de concurso,10451,questão de conhecimento específico,20,questão de conhecimento geral,30,questão de contabilidade,499,questão de contabilidade do setor publico,5,questão de controle externo,6,questão de criminologia,5,questão de defesa do consumidor,10,questão de design,116,questão de design de interiores,27,questão de design de moda,80,questão de dietética,40,questão de direito,3986,questão de direito administrativo,325,questão de direito administrativo e constitucional,10,questão de direito ambiental,21,questão de direito civil,233,questão de direito constitucional,296,questão de direito da criança e do adolescente,5,questão de direito da pessoa com deficiência,3,questão de direito do consumidor,5,questão de direito do trabalho,157,questão de direito eleitoral,7,questão de direito empresarial,168,questão de direito financeiro,28,questão de direito penal,227,questão de direito penal militar,6,questão de direito previdenciario,10,questão de direito processual civil,85,questão de direito processual do trabalho,15,questão de direito processual penal,81,questão de direito tributário,246,questão de direito urbanistico,8,questão de direitos humanos,4,questão de economia do setor público,4,questão de educação física,355,questão de enfermagem,382,questão de engenharia civil,132,questão de engenharia da computação,151,questão de engenharia de produção,92,questão de escriturário,10,questão de espanhol,925,questão de estatistica,55,questão de ética e legislação,4,questão de farmácia,317,questão de filosofia,428,questão de finanças públicas,9,questão de física,2113,questão de física médica,55,questão de fisioterapia,284,questão de fonoaudiologia,230,questão de frances,178,questão de geografia,1757,questão de gestão ambiental,92,questão de gestão de recursos humanos,67,questão de gestão financeira,135,questão de gestão hospitalar,108,questão de governança e gestão,40,questão de história,2279,questão de informática,242,questão de inglês,1882,questão de jornalismo,252,questão de legislação,361,questão de legislação estadual e institucional,8,questão de legislação penal,15,questão de legislação tributária,23,questão de licenciatura,57,questão de literatura,420,questão de literatura brasileira,20,questão de marketing,125,questão de matemática,4488,questão de matemática financeira,10,questão de medicina,2810,questão de medicina legal,25,questão de medicina veterinária,271,questão de modelagens e processo,10,questão de música,58,questão de necropsia,20,questão de neurologia pediátrica,30,questão de nutrição,381,questão de odontologia,233,questão de pedagogia,114,questão de planejamento de carreira e sucesso profissional,27,questão de planejamento e orçamento público,30,questão de português,5396,questão de princípios gerenciais de gorretagem,10,questão de processo legislativo,5,questão de processos gerenciais,74,questão de psicologia,467,questão de publicidade e propaganda,108,questão de química,1923,questão de raciocínio lógico,264,questão de radiologia,153,questão de redação,2,questão de relações internacionais,129,questão de saúde pública,75,questão de secretariado executivo,160,questão de segurança pública,5,questão de servico social,155,questão de serviço social,113,questão de sistema normativo anticorrupção,5,questão de sistemas de informação,56,questão de sociologia,239,questão de teatro,48,questão de tecnologia em agroindustria,25,questão de tecnologia em agronegocio,109,questão de tecnologia em análise e desenvolvimento de sistemas,30,questão de tecnologia em análise e desenvolvimentos,24,questão de tecnologia em estética e cosmética,29,questão de tecnologia em gestão e tecnologia da informação,30,questão de tecnologia em redes de computadores,83,questão de terapia ocupacional,204,questão de turismo,135,questão de vestibular,30306,questão de zootecnia,132,questão design de interiores,26,questão design gráfico,52,questão detran,96,questão do cefetmg,1816,questão do cfc,642,questão do enade,9127,questão do enare,50,questão do encceja,1141,questão do enem,3826,questão do ibfc,100,questão do ifba,62,questão do iff,53,questão do ifnmg,26,questão do ifpi,1167,questão do ime,40,questão do ita,554,questão do liceu piauiense,30,questão do mackenzie,1526,questão do revalida,1080,questão economia empresarial,29,questão enamed,90,questão engenharia,99,questão engenharia ambiental,98,questão engenharia civil,27,questão engenharia de alimentos,90,questão engenharia de controle e automacao,73,questão engenharia eletrica,73,questão engenharia florestal,82,questão engenharia mecânica,72,questão engenharia quimica,44,questão espm,239,questão faculdade dinamica,108,questão fadip,54,questão fagoc,50,questão famerp,700,questão faseh,60,questão fdsbc,100,questão fei,210,questão fiscal,40,questão fmj,120,questão fmo,90,questão funcern,240,questão fundatec,224,questão gastronomia,80,questão gestao comercial,80,questão gestão da produção,27,questão gestão de qualidade,81,questão gestão pública,79,questão gestão recursos humanos,25,questão iades,60,questão iave,89,questão ibade,107,questão ibest,40,questão ibfc,320,questão idib,40,questão ieses,190,questão ifce,90,questão ifmg,126,questão ifmt,130,questão ifsul,357,questão ifto,361,questão italiano,8,questão letras,65,questão lógica,5,questão logística,54,questão máxima,50,questão modelagem de processos,11,questão multidisciplinar,68,questão nucepe,46,questão objetiva,20,questão obras e postura,28,questão princípios gerenciais de corretagem,15,questão processo do trabalho,10,questão processo tributario,15,questão processos gerenciais,27,questão pucgo,186,questão pucrj,70,questão quadrix,120,questão slmandic,70,questão técnico agrícola,15,questão técnico de laboratório,10,questão tecnologia em alimentos,27,questão tecnologia em comércio exterior,27,questão tecnologia em design de interiores,27,questão tecnologia em design de moda,27,questão tecnologia em design gráfico,27,questão tecnologia em logística,27,questão tecnologia em manutenção industrial,27,questão tecnologia em marketing,26,questão tecnologia em saneamento ambiental,25,questão tecnologia estética e cosmetica,28,questão tecnologia seguranca do trabalho,56,questão tecnólogo de ti,30,questão teologia,81,questão ucb,106,questão udesc,106,questão uem,186,questão uepg,134,questão uesb,60,questão uespi,127,questão ufgd,187,questão ufpe,50,questão ufpr,70,questão ufsc,116,questão ufu,94,questão unemat,77,questão unifaminas,54,questão unifenas,128,questão unifil,29,questão unimontes,3,questão uninassau,90,questão unioeste,81,questão univesp,114,questão upe,1104,questão uri,84,questão urologia,15,questão web design,40,questões,63278,quimica,67,raciocínio lógico,7,radiologia,6,redacao,165,reflexão em texto,8,relações internacionais,4,religiao,5,resumo,5,revalida,67,rhinsight,8,saeb,2,santacasa,92,saude publica,2,secretariado executivo,6,seguranca do trabalho,2,serviço social,10,sesc,1,sexto ano,1,silabas,18,simulado,2,sistemas de informação,1,sisu,2,slmandic,2,sociologia,14,teatro,2,técnico agrícola,1,tecnologia em agroindustria,2,tecnologia em agronegocio,4,tecnologia em alimentos,1,tecnologia em comércio exterior,1,tecnologia em design de interiores,1,tecnologia em design de moda,1,tecnologia em design gráfico,1,tecnologia em gestão ambiental,2,tecnologia em gestão hospitalar,1,tecnologia em logística,1,tecnologia em marketing,1,teologia,2,terapia ocupacional,7,textos,45,textos paradidáticos,1,trechos,1,turismo,7,uber,1,ucb,10,udesc,14,uece,50,ueg,8,uel,25,uem,3,uema,11,uemg,13,uepg,4,uerj,73,uespi,3,ufam,3,ufc,2,ufes,2,uffs,4,ufg,1,ufgd,71,ufma,1,ufmg,1,ufpa,1,ufpi,2,ufpr,1,ufrgs,2,ufrn,2,ufsc,5,ufscar,1,uftm,188,unb,1,unemat,2,unesp,21,unicamp,22,unicentro,15,unicesumar,5,uniceub,4,unichristus,14,unifaminas,1,unifenas,8,unifesp,41,unifor,12,uninassau,3,uninove,1,unioeste,6,unip,3,unirg,13,unirv,3,unitins,6,univesp,2,upe,23,urbanismo,1,usp,54,vestibular,945,videos,5,vivo,1,vunesp,1,zootecnia,7,




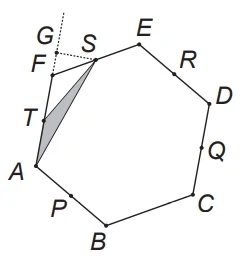
 pois esses segmentos paralelos a AB e ED, recém-traçados são equidistantes.
pois esses segmentos paralelos a AB e ED, recém-traçados são equidistantes.


 da área do triângulo APR, conforme visto no item b) e, portanto, sua área será
da área do triângulo APR, conforme visto no item b) e, portanto, sua área será 
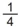 da área do retângulo P´AER´, portanto, sua área será
da área do retângulo P´AER´, portanto, sua área será 
 e, consequentemente, a área não sombreada é igual a
e, consequentemente, a área não sombreada é igual a 











COMENTÁRIOS