Prova concurso de Estatístico SEDUC/AM com Gabarito Concurso : SEDUC/AM Banca : Instituto Acesso Cargo : Estatístico Instituição : S...
Concurso: SEDUC/AM
Banca: Instituto Acesso
Cargo: Estatístico
Instituição: SEDUC/AM
Nível: Superior Completo
Sumário da prova:
- Língua Portuguesa (01 - 20)
- Legislação Específica (21 - 30)
- Contador (31 - 50)
- Engenheiro Civil (31 - 50)
- Engenheiro Eletricista (31 - 50)
- Fonoaudiólogo (31 - 50)
- Estatístico (31 - 50) - você está aqui
CONHECIMENTOS ESPECÍFICOS
QUESTÃO 31
(Instituto Acesso) Marque o item abaixo que apresenta o grau de liberdade da Média dos Quadrados dos Erros (MQR), utilizada no teste da Análise da Variância (ANOVA) de dois fatores. Para isso, considere que: a é o número de níveis do fator A; b é o número de níveis do fator B; n' é o número de réplicas em cada uma das ab células; n é o número de valores em todo o experimento.
A) (a-1)(b-1)
B) abn'
C) an'
D) ab(n’-1)
E) n'
Resposta.
(Instituto Acesso) Marque o item abaixo que apresenta o grau de liberdade da Média dos Quadrados dos Erros (MQR), utilizada no teste da Análise da Variância (ANOVA) de dois fatores. Para isso, considere que: a é o número de níveis do fator A; b é o número de níveis do fator B; n' é o número de réplicas em cada uma das ab células; n é o número de valores em todo o experimento.
A) (a-1)(b-1)
B) abn'
C) an'
D) ab(n’-1)
E) n'
Resposta.
QUESTÃO 32
(Instituto Acesso) Um estatístico pretende verificar a relação entre o nível de renda da população (em R$ milhões) de algumas cidades do Estado do Amazonas, com base no número de habitantes destas cidades (em milhares). Nesta verificação, será utilizado o modelo de regressão linear simples: ŷi = 3,4979 + 0,5781xi, sendo os coeficientes de regressão calculados pelo método dos mínimos quadrados, e considerando os seguintes valores:
Marque o item que apresenta o coeficiente de determinação desta regressão linear:
A) 0,7847
B) 0,9087
C) 0,9533
D) 0,9694
E) 0,9846
Resposta.
(Instituto Acesso) Um estatístico pretende verificar a relação entre o nível de renda da população (em R$ milhões) de algumas cidades do Estado do Amazonas, com base no número de habitantes destas cidades (em milhares). Nesta verificação, será utilizado o modelo de regressão linear simples: ŷi = 3,4979 + 0,5781xi, sendo os coeficientes de regressão calculados pelo método dos mínimos quadrados, e considerando os seguintes valores:
Marque o item que apresenta o coeficiente de determinação desta regressão linear:
A) 0,7847
B) 0,9087
C) 0,9533
D) 0,9694
E) 0,9846
Resposta.
QUESTÃO 33
(Instituto Acesso) Quando se deseja analisar o comportamento dos dados, o estatístico pode utilizar-se da distribuição de probabilidade ou da Função de Densidade de Probabilidade (FDP). Quanto às definições e propriedades das FDP, marque o item incorreto:
A) Na distribuição Uniforme Contínua:
para a ≤ x ≤ b, com valor esperado de X igual a
e variância de X igual a
B)Na distribuição Normal:
, para− ∞ < 𝒙 < +∞, com valor esperado de X igual a 𝝁 e variância de X igual a 𝝈², sendo −∞ < 𝝁 < +∞ e 𝝈 > 𝟎.
C) Na distribuição Exponencial:
, para 0 ≤ 𝑥 < ∞, sendo a variável aleatória X a distância entre as contagens sucessivas de um processo de Poisson, com média λ > 0.
D) Na distribuição Erlang:
, para x > 0 e r = 1, 2, ...; sendo a variável aleatória X o comprimento do intervalo até que r falhas ocorram em um processo de Poisson, com média λ > 0.
E) A distribuição Weibull:
, para x > 0, com parâmetro de escala δ > 0 e parâmetro de forma β > 0; usada frequentemente para modelar o tempo até uma falha de muitos sistemas físicos diferentes.
Resposta.
(Instituto Acesso) Quando se deseja analisar o comportamento dos dados, o estatístico pode utilizar-se da distribuição de probabilidade ou da Função de Densidade de Probabilidade (FDP). Quanto às definições e propriedades das FDP, marque o item incorreto:
A) Na distribuição Uniforme Contínua:
para a ≤ x ≤ b, com valor esperado de X igual a
e variância de X igual a
B)Na distribuição Normal:
, para− ∞ < 𝒙 < +∞, com valor esperado de X igual a 𝝁 e variância de X igual a 𝝈², sendo −∞ < 𝝁 < +∞ e 𝝈 > 𝟎.
C) Na distribuição Exponencial:
D) Na distribuição Erlang:
, para x > 0 e r = 1, 2, ...; sendo a variável aleatória X o comprimento do intervalo até que r falhas ocorram em um processo de Poisson, com média λ > 0.
E) A distribuição Weibull:
, para x > 0, com parâmetro de escala δ > 0 e parâmetro de forma β > 0; usada frequentemente para modelar o tempo até uma falha de muitos sistemas físicos diferentes.
Resposta.
Considerando a distribuição conjunta de probabilidades entre X e Y apresentada na Figura 1, responda às questões definidas em (34) e (35).
QUESTÃO 34
(Instituto Acesso) Marque o item abaixo que apresenta a seguinte distribuição marginal de probabilidade de X; P(X = 2):
A) 9,0108x10ˉ²
B) 0,18722
C) 0,09731
D) 0,94584
E) 0,06220
Resposta.
(Instituto Acesso) Marque o item abaixo que apresenta a seguinte distribuição marginal de probabilidade de X; P(X = 2):
A) 9,0108x10ˉ²
B) 0,18722
C) 0,09731
D) 0,94584
E) 0,06220
Resposta.
QUESTÃO 35
(Instituto Acesso) Marque o item abaixo que apresenta o E(Y):
A)0,605691
B) 3,135916
C) 0,194620
D) 0,180216
E) 0,248800
Resposta.
(Instituto Acesso) Marque o item abaixo que apresenta o E(Y):
A)0,605691
B) 3,135916
C) 0,194620
D) 0,180216
E) 0,248800
Resposta.
QUESTÃO 36
(Instituto Acesso) Visando analisar o tempo da vida útil das lâmpadas produzidas por dois fabricantes distintos (A e B), conforme oito amostras aleatórias coletadas para as lâmpadas de cada fabricante, apresentadas na Tabela 1, marque abaixo a opção incorreta quanto ao teste para verificação da possível diferença significativa entre as populações de A e B.
A) Em termos de possível diferença nas variâncias do tempo de vida útil das lâmpadas dos dois fabricantes, formula-se o teste
com uso da estatística F.
B) Em termos de média das diferenças da vida útil das lâmpadas dos dois fabricantes, formula-se o teste 𝐻0: 𝜇𝐷 = 0, com cálculo da estatística t, sendo 𝜇𝐷 a média das diferenças.
C) Em termos de diferença entre as médias da vida útil das lâmpadas dos dois fabricantes, formula-se o teste 𝑯𝟎: 𝝁𝑨 = 𝝁𝑩, com uso do teste t para variância agrupada se rejeitar H0 no teste especificado no item (a) desta questão.
D) Em termos da média da vida útil das lâmpadas do fabricante A ser diferente de 400 horas, formula-se o teste 𝐻0: 𝜇𝐴 = 400ℎ𝑜𝑟𝑎𝑠, com o uso do teste t de student e (n – 1) graus de liberdade.
E) Em termos da média da vida útil das lâmpadas do fabricante B ser menor do que 400 horas, formula-se o teste 𝐻0: 𝜇𝐵 ≥ 400ℎ𝑜𝑟𝑎𝑠, com o uso do teste t de student e (n – 1) graus de liberdade.
Resposta.
(Instituto Acesso) Visando analisar o tempo da vida útil das lâmpadas produzidas por dois fabricantes distintos (A e B), conforme oito amostras aleatórias coletadas para as lâmpadas de cada fabricante, apresentadas na Tabela 1, marque abaixo a opção incorreta quanto ao teste para verificação da possível diferença significativa entre as populações de A e B.
A) Em termos de possível diferença nas variâncias do tempo de vida útil das lâmpadas dos dois fabricantes, formula-se o teste
com uso da estatística F.
B) Em termos de média das diferenças da vida útil das lâmpadas dos dois fabricantes, formula-se o teste 𝐻0: 𝜇𝐷 = 0, com cálculo da estatística t, sendo 𝜇𝐷 a média das diferenças.
C) Em termos de diferença entre as médias da vida útil das lâmpadas dos dois fabricantes, formula-se o teste 𝑯𝟎: 𝝁𝑨 = 𝝁𝑩, com uso do teste t para variância agrupada se rejeitar H0 no teste especificado no item (a) desta questão.
D) Em termos da média da vida útil das lâmpadas do fabricante A ser diferente de 400 horas, formula-se o teste 𝐻0: 𝜇𝐴 = 400ℎ𝑜𝑟𝑎𝑠, com o uso do teste t de student e (n – 1) graus de liberdade.
E) Em termos da média da vida útil das lâmpadas do fabricante B ser menor do que 400 horas, formula-se o teste 𝐻0: 𝜇𝐵 ≥ 400ℎ𝑜𝑟𝑎𝑠, com o uso do teste t de student e (n – 1) graus de liberdade.
Resposta.
QUESTÃO 37
(Instituto Acesso) Algumas análises podem ser realizadas na aplicação de métodos estatísticos multivariados, sendo que existem alguns testes para comparar os vetores de médias de várias amostras multivariadas, com exceção do(a):
A)Teste de Van Valen.
B) Traço de Lawley Hotteling.
C) Teste Lambda de Wilks.
D) Estatística Traço de Pillai.
E) Teste da Maior Raiz de Roy.
Resposta.
(Instituto Acesso) Algumas análises podem ser realizadas na aplicação de métodos estatísticos multivariados, sendo que existem alguns testes para comparar os vetores de médias de várias amostras multivariadas, com exceção do(a):
A)Teste de Van Valen.
B) Traço de Lawley Hotteling.
C) Teste Lambda de Wilks.
D) Estatística Traço de Pillai.
E) Teste da Maior Raiz de Roy.
Resposta.
QUESTÃO 38
(Instituto Acesso) Com base no seguinte conjunto de dados, marque o item que apresenta, respectivamente, os valores da média, da mediana, e da moda: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
A) 5,5; 5,5; não há moda.
B) 5,5; 5; não há moda.
C) 5,5; 5,5; 5.
D) 5,5; 5; 5.
E) 5; 5,5; todos os números (multimodal).
Resposta.
(Instituto Acesso) Com base no seguinte conjunto de dados, marque o item que apresenta, respectivamente, os valores da média, da mediana, e da moda: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
A) 5,5; 5,5; não há moda.
B) 5,5; 5; não há moda.
C) 5,5; 5,5; 5.
D) 5,5; 5; 5.
E) 5; 5,5; todos os números (multimodal).
Resposta.
QUESTÃO 39
(Instituto Acesso) Considerando que X1, X2,..., Xn forem variáveis aleatórias independentes, com funções geradoras de momento respectivamente definidas por Mx1(t), Mx2(t),...,Mxn(t). Se Y = X1 + X2 + ... + Xn, então a função geradora de momento de Y será dada por:
A) MY(t) = [Mx1(t)] + [Mx2(t)] + ... + [Mxn(t)]
B) MY(t) = [Mxn(t)] - [Mxn-1(t)] - ... - [Mx1(t)]
C) MY(t) = [Mx1(t)] x [Mx2(t)] x ... x [Mxn(t)]
D) MY(t) = [Mxn(t)] + [Mx1(t)]/2
E) MY(t) = [Mxn(t)] + [Mx1(t)]/2
Resposta.
(Instituto Acesso) Considerando que X1, X2,..., Xn forem variáveis aleatórias independentes, com funções geradoras de momento respectivamente definidas por Mx1(t), Mx2(t),...,Mxn(t). Se Y = X1 + X2 + ... + Xn, então a função geradora de momento de Y será dada por:
A) MY(t) = [Mx1(t)] + [Mx2(t)] + ... + [Mxn(t)]
B) MY(t) = [Mxn(t)] - [Mxn-1(t)] - ... - [Mx1(t)]
C) MY(t) = [Mx1(t)] x [Mx2(t)] x ... x [Mxn(t)]
D) MY(t) = [Mxn(t)] + [Mx1(t)]/2
E) MY(t) = [Mxn(t)] + [Mx1(t)]/2
Resposta.
QUESTÃO 40
(Instituto Acesso) Uma série temporal é um conjunto de observações ordenadas no tempo e que apresentam dependência serial. Quanto aos modelos Box & Jenkins, marque o item incorreto:
A) As metodologias de modelos Box & Jenkins buscam capturar a estrutura de dependência entre os valores observados, restando uma série de resíduos com um comportamento aleatório com valor esperado igual a zero.
B) Os modelos Box & Jenkins analisam séries temporais estacionárias, buscando identificar algum padrão que ajude entender o comportamento da série.
C) A identificação do modelo representativo seguindo esta metodologia ocorre com base em autocorrelações e correlações parciais para as séries estacionárias.
D) Podem ser realizados testes de Raiz Unitária: Dickey-Fuller (DF), Dickey-Fuller Aumentado (ADF), Phillips e Perron (PP), Dickey-Pantula; sendo que quando a série temporal possui Raiz Unitária ela é definida como Não Estacionária.
E) Na escolha do melhor modelo para explicar o comportamento da série de dados, pode ser utilizado o critério Akaike e o critério Schwarz. Quanto maiores forem os valores destes critérios em um determinado modelo analisado, melhor será o referido modelo.
Resposta.
(Instituto Acesso) Uma série temporal é um conjunto de observações ordenadas no tempo e que apresentam dependência serial. Quanto aos modelos Box & Jenkins, marque o item incorreto:
A) As metodologias de modelos Box & Jenkins buscam capturar a estrutura de dependência entre os valores observados, restando uma série de resíduos com um comportamento aleatório com valor esperado igual a zero.
B) Os modelos Box & Jenkins analisam séries temporais estacionárias, buscando identificar algum padrão que ajude entender o comportamento da série.
C) A identificação do modelo representativo seguindo esta metodologia ocorre com base em autocorrelações e correlações parciais para as séries estacionárias.
D) Podem ser realizados testes de Raiz Unitária: Dickey-Fuller (DF), Dickey-Fuller Aumentado (ADF), Phillips e Perron (PP), Dickey-Pantula; sendo que quando a série temporal possui Raiz Unitária ela é definida como Não Estacionária.
E) Na escolha do melhor modelo para explicar o comportamento da série de dados, pode ser utilizado o critério Akaike e o critério Schwarz. Quanto maiores forem os valores destes critérios em um determinado modelo analisado, melhor será o referido modelo.
Resposta.
QUESTÃO 41
(Instituto Acesso) Será utilizada uma amostragem aleatória para a realização de uma pesquisa com a população sobre o seu nível de satisfação com as políticas realizadas pelo governo do estado. Esta pesquisa pretende alcançar um erro de estimação de ±0,1052, com um nível de significância de 10%. Sabe-se que na última pesquisa o percentual de satisfação com as políticas do governo do estado variava entre 40% e 60%. Marque o item abaixo que apresenta o tamanho (n) mínimo da amostra que esta amostra deve estar dimensionada.
A) n = 87
B) n = 74
C) n = 62
D) n = 38
E) n = 36
Resposta.
(Instituto Acesso) Será utilizada uma amostragem aleatória para a realização de uma pesquisa com a população sobre o seu nível de satisfação com as políticas realizadas pelo governo do estado. Esta pesquisa pretende alcançar um erro de estimação de ±0,1052, com um nível de significância de 10%. Sabe-se que na última pesquisa o percentual de satisfação com as políticas do governo do estado variava entre 40% e 60%. Marque o item abaixo que apresenta o tamanho (n) mínimo da amostra que esta amostra deve estar dimensionada.
A) n = 87
B) n = 74
C) n = 62
D) n = 38
E) n = 36
Resposta.
QUESTÃO 42
(Instituto Acesso) Uma empresa de transporte rodoviário verificou que a distância média percorrida por dia por cada caminhão variava, com 95% de confiança, entre 36,62km e 40,38km. Considerando que na definição deste intervalo foi utilizada uma amostra de 60 caminhões e que esta amostra gerou uma média de 38,5, marque o item que apresenta o valor do desvio-padrão amostral.
A) 7,19
B) 7,22
C) 7,25
D) 7,28
E) 7,31
Resposta.
(Instituto Acesso) Uma empresa de transporte rodoviário verificou que a distância média percorrida por dia por cada caminhão variava, com 95% de confiança, entre 36,62km e 40,38km. Considerando que na definição deste intervalo foi utilizada uma amostra de 60 caminhões e que esta amostra gerou uma média de 38,5, marque o item que apresenta o valor do desvio-padrão amostral.
A) 7,19
B) 7,22
C) 7,25
D) 7,28
E) 7,31
Resposta.
QUESTÃO 43
(Instituto Acesso) Num processo produtivo foi selecionada uma amostra de 270 peças, selecionadas ao final de sua linha de produção; destas, 10% estavam com algum tipo de inconsistência com os padrões necessários de qualidade. Com 90% de confiança, determine os valores (limite inferior e limite superior) mais próximos do intervalo, referente à população da proporção das peças geradas neste processo produtivo que estão consistentes com os padrões necessários de qualidade.
A) 𝐼𝐶𝜋 = [0,89; 0,91]
B) 𝐼𝐶𝜋 = [0,87; 0,93]
C) 𝐼𝐶𝜋 = [0,85; 0,95]
D) 𝐼𝐶𝜋 = [0,07; 0,13]
E) 𝐼𝐶𝜋 = [0,05; 0,15]
Resposta.
(Instituto Acesso) Num processo produtivo foi selecionada uma amostra de 270 peças, selecionadas ao final de sua linha de produção; destas, 10% estavam com algum tipo de inconsistência com os padrões necessários de qualidade. Com 90% de confiança, determine os valores (limite inferior e limite superior) mais próximos do intervalo, referente à população da proporção das peças geradas neste processo produtivo que estão consistentes com os padrões necessários de qualidade.
A) 𝐼𝐶𝜋 = [0,89; 0,91]
B) 𝐼𝐶𝜋 = [0,87; 0,93]
C) 𝐼𝐶𝜋 = [0,85; 0,95]
D) 𝐼𝐶𝜋 = [0,07; 0,13]
E) 𝐼𝐶𝜋 = [0,05; 0,15]
Resposta.
QUESTÃO 44
(Instituto Acesso) Os gerentes de um setor da fábrica analisam periodicamente as peças produzidas para tentar detectar possíveis variações em relação ao seu valor padrão. Sabe-se que uma das dimensões de uma peça fabricada neste setor é de 5,00cm, e se quer testar se a média desta dimensão é igual ou difere de seu valor padrão.
O desvio-padrão da dimensão é conhecido e igual a 0,05cm. O teste será feito com uma amostra de 4 unidades da peça e possuirá 5% de significância. Caso o verdadeiro valor da média seja de 4,95, verifique a probabilidade de que aceitemos que a média não difere de 5,00 e marque o item abaixo que apresenta o valor da potência do teste, aproximadamente.
A) 60,25%
B) 51,60%
C) 50,05%
D) 48,40%
E) 39,75%
Resposta.
(Instituto Acesso) Os gerentes de um setor da fábrica analisam periodicamente as peças produzidas para tentar detectar possíveis variações em relação ao seu valor padrão. Sabe-se que uma das dimensões de uma peça fabricada neste setor é de 5,00cm, e se quer testar se a média desta dimensão é igual ou difere de seu valor padrão.
O desvio-padrão da dimensão é conhecido e igual a 0,05cm. O teste será feito com uma amostra de 4 unidades da peça e possuirá 5% de significância. Caso o verdadeiro valor da média seja de 4,95, verifique a probabilidade de que aceitemos que a média não difere de 5,00 e marque o item abaixo que apresenta o valor da potência do teste, aproximadamente.
A) 60,25%
B) 51,60%
C) 50,05%
D) 48,40%
E) 39,75%
Resposta.
QUESTÃO 45
(Instituto Acesso) Sabendo que X é uma variável aleatória, podendo assumir três possíveis valores com iguais probabilidades: -2, 0, 2. É conhecida a função de probabilidade de Y, uniforme discreta, como sendo: 𝑝𝑦/𝑥(𝑦/𝑋 = 𝑥). Esta função pode assumir os valores (x-2), x, (x+2) com iguais probabilidades. Marque o item abaixo que apresenta, respectivamente os seguintes valores: variância de X, variância de Y, correlação (valor aproximado) entre X e Y.
A) 8/3; 48/9; 0,4472
B) 48/9; 8/3; 2/9
C) 8/3; 48/9; 0,7071
D) 8/3; 2/9; 0,4472
E) 48/9; 2/9; 8/3
Resposta.
(Instituto Acesso) Sabendo que X é uma variável aleatória, podendo assumir três possíveis valores com iguais probabilidades: -2, 0, 2. É conhecida a função de probabilidade de Y, uniforme discreta, como sendo: 𝑝𝑦/𝑥(𝑦/𝑋 = 𝑥). Esta função pode assumir os valores (x-2), x, (x+2) com iguais probabilidades. Marque o item abaixo que apresenta, respectivamente os seguintes valores: variância de X, variância de Y, correlação (valor aproximado) entre X e Y.
A) 8/3; 48/9; 0,4472
B) 48/9; 8/3; 2/9
C) 8/3; 48/9; 0,7071
D) 8/3; 2/9; 0,4472
E) 48/9; 2/9; 8/3
Resposta.
QUESTÃO 46
(Instituto Acesso) A vida útil, em milhares de horas, de um eletrodoméstico pode ser representada por uma variável aleatória contínua X, com a seguinte função densidade de probabilidade:
Marque o item abaixo que apresenta, respectivamente, o valor de k e a probabilidade que uma lâmpada funcione pelo menos 75.000 horas, dado que já funcionou 50.000 horas.
A) K = 5, probabilidade = 2/3.
B) K = 10, probabilidade = 1/3.
C) K = 10, probabilidade = 2/3.
D) K = 25, probabilidade = 1/3.
E) K = 25, probabilidade = 2/3.
Resposta.
(Instituto Acesso) A vida útil, em milhares de horas, de um eletrodoméstico pode ser representada por uma variável aleatória contínua X, com a seguinte função densidade de probabilidade:
Marque o item abaixo que apresenta, respectivamente, o valor de k e a probabilidade que uma lâmpada funcione pelo menos 75.000 horas, dado que já funcionou 50.000 horas.
A) K = 5, probabilidade = 2/3.
B) K = 10, probabilidade = 1/3.
C) K = 10, probabilidade = 2/3.
D) K = 25, probabilidade = 1/3.
E) K = 25, probabilidade = 2/3.
Resposta.
QUESTÃO 47
(Instituto Acesso) Um modelo de Regressão Múltipla tem a sua equação estimada como
sendo
Sobre este modelo pode-se afirmar que:
A) No teste de significância global de regressão da amostra deve ser analisada separadamente a possibilidade de 𝛽𝑖 (i = 2 e 3) ser diferente de zero, e desta forma 𝐻0:𝛽2 = 0 e 𝐻0:𝛽3 = 0.
B) No teste de significância global de regressão da amostra deve ser utilizada a estatística t de student para a verificação se o valor calculado da estatística t supera, ou não, seu valor crítico de significância determinado para o teste.
C) O teste, por meio da técnica da Análise de Variância (ANOVA) tem grau de liberdade igual a 3 para a fonte de variação proveniente da Regressão.
D) O teste, por meio da técnica da Análise de Variância (ANOVA) tem grau de liberdade igual a (n-3) para a fonte de variação proveniente dos Resíduos.
E) A estimativa do Intervalo de Confiança para cada um dos coeficientes é determinado com o valor estimado de cada coeficiente somado/subtraído da sua margem de erro, esta formada pelo valor da estatística normal padronizada (estatística z), multiplicada pelo erro padrão de cada um dos seus coeficientes.
Resposta.
(Instituto Acesso) Um modelo de Regressão Múltipla tem a sua equação estimada como
sendo
Sobre este modelo pode-se afirmar que:
A) No teste de significância global de regressão da amostra deve ser analisada separadamente a possibilidade de 𝛽𝑖 (i = 2 e 3) ser diferente de zero, e desta forma 𝐻0:𝛽2 = 0 e 𝐻0:𝛽3 = 0.
B) No teste de significância global de regressão da amostra deve ser utilizada a estatística t de student para a verificação se o valor calculado da estatística t supera, ou não, seu valor crítico de significância determinado para o teste.
C) O teste, por meio da técnica da Análise de Variância (ANOVA) tem grau de liberdade igual a 3 para a fonte de variação proveniente da Regressão.
D) O teste, por meio da técnica da Análise de Variância (ANOVA) tem grau de liberdade igual a (n-3) para a fonte de variação proveniente dos Resíduos.
E) A estimativa do Intervalo de Confiança para cada um dos coeficientes é determinado com o valor estimado de cada coeficiente somado/subtraído da sua margem de erro, esta formada pelo valor da estatística normal padronizada (estatística z), multiplicada pelo erro padrão de cada um dos seus coeficientes.
Resposta.
QUESTÃO 48
(Instituto Acesso) No momento da identificação dos modelos Box & Jenkins para séries temporais, são utilizados os padrões gerados nos correlogramas para a escolha das especificações funcionais destes modelos. Desta maneira, marque o item abaixo que apresenta o possível modelo relacionado ao seguinte fato: o correlograma tem padrão de redução exponencial, assim como o seu correlograma parcial.
A) Autoregressivo – AR(1)
B) Autoregressivo – AR(2)
C) Média Móvel – MA(1)
D) Média Móvel – MA(2)
E) Autoregressivo com Média Móvel – ARMA (1,1)
Resposta.
(Instituto Acesso) No momento da identificação dos modelos Box & Jenkins para séries temporais, são utilizados os padrões gerados nos correlogramas para a escolha das especificações funcionais destes modelos. Desta maneira, marque o item abaixo que apresenta o possível modelo relacionado ao seguinte fato: o correlograma tem padrão de redução exponencial, assim como o seu correlograma parcial.
A) Autoregressivo – AR(1)
B) Autoregressivo – AR(2)
C) Média Móvel – MA(1)
D) Média Móvel – MA(2)
E) Autoregressivo com Média Móvel – ARMA (1,1)
Resposta.
QUESTÃO 49
(Instituto Acesso) Quanto às propriedades da Função Geradora de Momentos (FGM), marque o item incorreto:
A) A FGM é única para cada variável aleatória e determina completamente a sua distribuição; pela função densidade de probabilidade ou pela função de distribuição acumulada.
B) A FGM é dada por:
para a variável aleatória X contínua.
C) A existência do k-ésimo momento de uma distribuição caracteriza a existência dos momentos de ordem inferior à k.
D) A FGM é dada por:
para a variável aleatória X discreta.
E) O primeiro momento caracteriza a tendência Central (média), o segundo momento caracteriza a Dispersão (Variância), o terceiro momento a Curtose e o quarto a Assimetria.
Resposta.
(Instituto Acesso) Quanto às propriedades da Função Geradora de Momentos (FGM), marque o item incorreto:
A) A FGM é única para cada variável aleatória e determina completamente a sua distribuição; pela função densidade de probabilidade ou pela função de distribuição acumulada.
B) A FGM é dada por:
para a variável aleatória X contínua.
C) A existência do k-ésimo momento de uma distribuição caracteriza a existência dos momentos de ordem inferior à k.
D) A FGM é dada por:
para a variável aleatória X discreta.
E) O primeiro momento caracteriza a tendência Central (média), o segundo momento caracteriza a Dispersão (Variância), o terceiro momento a Curtose e o quarto a Assimetria.
Resposta.
(Instituto Acesso) Dois amigos resolveram analisar o tempo em que se deslocavam ao trabalho (em minutos) e cada um realizou o monitoramento do seu percurso. João marcou seu tempo ao longo de oito dias do trajeto realizado ao trabalho e José marcou seu tempo em seis dias. Diante dos dados amostrais apresentados na Tabela abaixo, marque o item que apresenta uma possível resposta para o teste de verificação da existência de evidência de alguma diferença significativa nas variâncias do tempo de deslocamento do trabalho de José e João. Utilize:
A) Rejeita H0 ao nível de significância de 0,5%, com o uso da estatística z para o teste.
B) Rejeita H0 ao nível de significância de 1%, com o uso da estatística F para o teste.
C) Não Rejeita H0 ao nível de significância de 2,5%, com o uso da estatística F para o teste.
D) Rejeita H0 ao nível de significância de 5%, com o uso da estatística z para o teste.
E) Não Rejeita H0 ao nível de significância de 10%, com o uso da estatística F para o teste.
A) Rejeita H0 ao nível de significância de 0,5%, com o uso da estatística z para o teste.
B) Rejeita H0 ao nível de significância de 1%, com o uso da estatística F para o teste.
C) Não Rejeita H0 ao nível de significância de 2,5%, com o uso da estatística F para o teste.
D) Rejeita H0 ao nível de significância de 5%, com o uso da estatística z para o teste.
E) Não Rejeita H0 ao nível de significância de 10%, com o uso da estatística F para o teste.
Dados para essa prova de Conhecimento Específico.






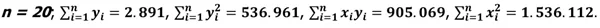



















COMENTÁRIOS