Prova ITA 2023 (2ª Fase) com Gabarito - Prova ITA 2023 (1ª Fase) com Gabarito 2ª FASE - 1º DIA MATEMÁTICA ITA 2023 - QUESTÃO 01 Sejam...
Prova ITA 2023 (2ª Fase) com Gabarito
2ª FASE - 1º DIA
MATEMÁTICA
ITA 2023 - QUESTÃO 01
Sejam a e b números reais positivos. Considere o sistema linear nas incógnitas x, y e z:
Sabendo que esse sistema admite solução não trivial, determine b em função de a. Determine o conjunto solução do sistema para 
ITA 2023 - QUESTÃO 02
Considere as seguintes matrizes:

Determine os números a ∈ R tais que a matriz
M = α²A + αB + C é invertível.
ITA 2023 - QUESTÃO 04
Considere o polinômio p(x) = x⁴ – x³ + x² – x + 1.
Determine o quociente e o resto da divisão do polinômio q(x) = x¹⁰ – 1 por p(x) e encontre todas as raízes complexas de p(x).
ITA 2023 - QUESTÃO 05
Sejam A = cos(α) + cos(β) e B = sen(α) – sen(β) com α, β ∈ R. Calcule sen(α – β) em função de A e B, sabendo que A e B não são ambos nulos.
ITA 2023 - QUESTÃO 06
Considere um triângulo ABC tal que  = 4,
= 4,  = 5 e BÂC = 60°. Seja D um ponto no lado
= 5 e BÂC = 60°. Seja D um ponto no lado  tal que
tal que  = 1.
= 1.
Encontre o raio do círculo inscrito no triângulo BCD.
ITA 2023 - QUESTÃO 07
Determine os Pontos P pertencentes à elipse E definida pela equação  tais que os segmentos de reta que ligam P aos focos de E formam um ângulo de 60°.
tais que os segmentos de reta que ligam P aos focos de E formam um ângulo de 60°.
ITA 2023 - QUESTÃO 08
Um cilindro equilátero é apoiado sobre uma de suas bases e parcialmente preenchido com água. Quando uma esfera é colocada em seu interior, de modo a tocar o fundo, o nível de água atinge a altura do cilindro.
Se o raio da esfera é igual ao raio da base do cilindro e o volume de água é 
determine a área da superfície lateral do cilindro e o volume da esfera.
ITA 2023 - QUESTÃO 09
Um triângulo tem perímetro 20 o seus ângulos internos α, β e γ satisfazem a igualdade sen(α) + sen(β) + sen(γ) = 2. Sabendo que um dos lados desse triângulo mede 8, determine a medida dos outros dois lados.
ITA 2023 - QUESTÃO 10
Em um decágono convexo, de quantas formas podemos escolher duas diagonais que não se interceptam?
QUÍMICA
ITA 2023 - QUESTÃO 11
Considere dois líquidos voláteis, A e B, que são completamente miscíveis entre si e que formam uma solução ideal em toda a amplitude de concentrações.
Esses líquidos são adicionados a um tanque fechado, inicialmente sob vácuo, e mantido em temperatura constante (T), na proporção molar 1:1. Considere que a mistura causa um abaixamento na pressão de vapor do líquido A igual a 40 Torr e que a pressão de vapor do líquido B puro é igual a 20 Torr.
Determine os valores numéricos:
a) da pressão de vapor do líquido A puro na temperatura T;
b) da pressão de vapor da solução, depois de atingido o equilíbrio do sistema;
e) da composição molar da fase vapor em equilíbrio com a fase líquida presente no tanque.
ITA 2023 - QUESTÃO 12
O ácido fórmico pode ser obtido por meio de uma reação de duas etapas. Na primeira etapa, em temperatura de 200°C e pressão de 10 atm, monóxido de carbono e hidróxido de sódio reagem. Na segunda, o produto dessa primeira etapa reage com ácido sulfúrico, formando-se oácido fórmico.
Sobre esse processo, apresente:
a) a fórmula estrutural do produto gerado na primeiraetapa;
b) a equação química balanceada da primeira etapa;
c) a equação química balanceada da segunda etapa.
ITA 2023 - QUESTÃO 13
Um determinado sistema consiste em dois sólidos, A e B, cada qual com uma quantidade igual a 1 mol.
Considere que os sólidos estão fisicamente separados, mas em contato térmico por meio de uma parede condutora de calor, a qual garante que estejam em equilíbrio térmico em todos os instantes. A temperatura inicial desse sistema é igual a –10°C.
O sistema é aquecido até atingir a temperatura de 20°C. A temperatura de fusão de A é igual a 0°C e a de B é igual a 10°C. Considere ainda os dados a seguir.
I. Variação de entalpia de fusão, de A, ΔHfusão(A) = 1kJ mol–1, e de B, ΔHfusão(B) = 2 kJ mol–1;
II. Capacidade calorífica molar sob pressão constante, de A sólido, Cp,sólido(A) = 30 J mol–1K–1, e de B sólido, Cp,sólido(B) = 20J mol–1K–1;
III. Capacidade calorífica molar sob pressão constante, de A líquido, Cp,líquido(A) = 50 J mol⁻¹K⁻¹, e de B líquido, Cp,líquido(B) = 100 J mol⁻¹K⁻¹.
Desenhe um gráfico da temperatura do sistema, em °C, em função da quantidade de calor fornecida, em kJ, indicando o fenômeno físico e o valor numérico da quantidade de calor fornecida em cada etapa do processo de aquecimento, até a temperatura final ser atingida.
ITA 2023 - QUESTÃO 14
Duas soluções aquosas, contendo os cátions genéricos, A⁺ e B⁺, são preparadas com as concentrações iniciais descritas a seguir.
Solução 1: [A⁺] = 2 x 10⁻² mol L⁻¹ e [B⁺] = 1 x 10⁻⁴ mol L⁻¹.
Solução 2: [A⁺] = 5 x 10⁻² mol L⁻¹ e [B⁺] = 1 x 10⁻³ mol L⁻¹.
A cada uma dessas soluções são adicionadas quantidades progressivas de um ânion C⁻, sem variação significativa do volume das soluções. Considere que os produtos de solubilidade dos sólidos AC(s) e BC(s) são iguais a 1 x 10⁻⁷ e 1 x 10⁻⁹, respectivamente.
Com base nessas informações, determine o que se pede para a solução 1 e para a solução 2.
a) Qual sólido será formado primeiro com a adição progressiva de C⁻ a cada uma das soluções? Justifique a sua resposta.
b) Conforme C⁻ é progressivamente adicionado, o segundo sólido começa a se formar. Nesse momento, qual é a concentração em solução do cátion desse primeiro sólido precipitado em cada solução?
ITA 2023 - QUESTÃO 15
Uma amostra de 5,480g de uma mistura de óxido e carbonato de um mesmo metal (com um estado de oxidação igual a +2 nesses compostos) é completamente dissolvida em excesso de ácido clorídrico. Nesse processo, 0,448L (condições normais) de gás são liberados.
Com base nessas informações, determine os valores numéricos
a) da composição da mistura, em frações mássicas, se a quantidade em mol de carbonato na mistura é duas vezes maior do que a quantidade do óxido;
b) da concentração molar do sal formado na solução resultante, se o volume final da dissolução é igual a 200 mL.
ITA 2023 - QUESTÃO 16
Suponha que, em medições experimentais realizadas no espaço sideral, foi descoberto um sistema formado de gás hidrogênio atômico excitado. A energia desse hidrogênio excitado é igual a –0,34 meV, fazendo com que o sistema emita um espectro de ondas eletromagnéticas de forma aparentemente contínua. Considere o modelo do átomo proposto por Bohr para descrever esse sistema.
Considere, ainda, que a energia do átomo de hidrogênio no estado fundamental é –13,6 eV e que o raio do átomo de hidrogênio no estado fundamental é igual a 53 pm.
Acerca desse sistema, determine o que se pede a seguir.
a) Qual é o nível de energia no qual os átomos de hidrogênio excitados se encontram?
b) Qual é o raio da órbita do elétron ao redor do próton nesses átomos de hidrogênio?
e) Qual é a razão entre a velocidade do elétron do átomo de hidrogênio no estado fundamental e no estado excitado?
ITA 2023 - QUESTÃO 17
A primeira determinação experimental do tamanho de um núcleo foi feita a partir dos resultados do espalhamento de Rutherford de partículas α.
Os resultados evidenciaram uma dependência entre o raio nuclear (R) e o número de massa (A), através da relação:
em que R0 é uma constante.
Com base nessas informações, calcule o valor numérico:
a) da densidade nuclear para o 29Cu⁶³, considerando que o raio para 30Zn⁶⁴ é 4,8 x 10⁻¹⁵m;
b) da razão entre os raios nucleares do isótopo de magnésio 12Mg²⁴ e do isótopo de ósmio 76Os¹⁹²;
c) da densidade nuclear para o seabórgio 106Sg²⁷¹, comparando-a com o valor da densidade nuclear do 29Cu⁶³ obtida no item (a) acima.
ITA 2023 - QUESTÃO 18
O método de obtenção de magnésio metálico consiste nas seguintes etapas:
I. Uma amostra de carbonato de cálcio sólido é aquecida a altas temperaturas, formando um produto sólido A e um gasoso B.
II. Em seguida, o sólido A é tratado com água do mar, formando-se um hidróxido pouco solúvel que se ioniza formando os produtos C e D.
III. Os ânions D reagem com cátions Mg2+ da água do mar. O resultado é um precipitado E.
IV. O composto E é separado por filtração e dissolvido por meio da adição de uma solução aquosa de ácido clorídrico.
V. A seguir, o solvente da solução é evaporado, obtendo-se o sal iônico F seco.
VI. Finalmente, o sal F é submetido a uma eletrólise ígnea.
Determine o que se pede.
a) Apresente as equações químicas balanceadas que representam as reações, identificando os produtos A, B, C, D, E e F formados.
b) Em relação à eletrólise ígnea, mostre as semiequações que representam as semirreações que ocorreram no anodo e no catodo, assim como a reação global.
ITA 2023 - QUESTÃO 19
Apresente os compostos orgânicos formados a partir das reações do etanoato de metila com os seguintes reagentes:
I. solução aquosa de ácido clorídrico.
II. solução aquosa de hidróxido de sódio.
III. amônia gasosa.
IV. Li(AlH4) dissolvido em dietiléter, seguido da adição de uma solução aquosa ácida.
ITA 2023 - QUESTÃO 20
Considere o composto de fórmula C4H8.
Apresente:
a) os seis isômeros estruturais e geométricos;
b) a fórmula estrutural dos produtos dibromados formados nas reações de cada um desses seis isômeros com Br2. Considere que as condições das reações são adequadas para que ocorram de forma completa e produtos dibromados sejam gerados.
2ª FASE - 2º DIA
FÍSICA
ITA 2023 - QUESTÃO 01
Um bloco cúbico de aresta l = 4,5 cm desliza, sob o efeito da gravidade, sobre um plano inclinado de ângulo α = 60° relativamente à horizontal. O deslizamento acontece com as normais de duas de suas faces sempre paralelas à direção do movimento.
Para estudar o movimento, um observador usa uma máquina fotográfica que captura em uma mesma imagem a posição do bloco em instantes diferentes. Para isso, a câmera é programada para abrir e fechar o diafragma periodicamente, a cada intervalo de tempo ∆t = 0,2 s. O tempo de exposição δt, isto é, o tempo em que o diafragma permanece aberto, é tal que δt ≪ ∆t.
O disparo da câmera é sincronizado com o movimento, de modo que a primeira exposição acontece no instante em que o bloco é solto. A foto registra quatro pontos, que correspondem à posição do objeto em diferentes instantes. O experimentador extrai da foto a distância entre pontos adjacentes, ∆xn = xn – xn – 1, com n = 1, 2 e 3.
Considere que a foto capta o perfil lateral do plano inclinado sem distorções ópticas ou efeitos de paralaxe. Em seguida, faça o que se pede:
a) se ∆x3 = 0,75 m. determine os valores de ∆x2, ∆x1 e o deslocamento total do bloco;
b) estime o valor do coeficiente de atrito cinético entre a superfície do bloco e do plano inclinado;
c) considere agora que δt ainda é pequeno, mas seu efeito já não é mais desprezível. Determine o valor de δt para que, na quarta captura, a imagem seja um retângulo de dimensões l por 2l.
ITA 2023 - QUESTÃO 02
Considere uma partícula P1, de massa m1, inicialmente em repouso. Em seguida, essa partícula é acelerada por uma força constante  durante um intervalo de tempo ∆t1.
durante um intervalo de tempo ∆t1.
Após este intervalo de tempo, P1 move-se livremente sem atrito por um plano, até colidir com uma partícula P2, de massa m2 = 2m1. Após a colisão, P2 sai em uma trajetória que faz um ângulo de θ = π/6 rad com relação à trajetória inicial (pré-colisão) de P1.
Após um breve deslocamento, uma força constante  com direção contrária à da velocidade da partícula P2, atua durante um intervalo de tempo ∆t2 = √3∆t 1 até a parada total de P2.
com direção contrária à da velocidade da partícula P2, atua durante um intervalo de tempo ∆t2 = √3∆t 1 até a parada total de P2.
Sabendo que a colisão entre P1 e P2 é inelástica e resulta em uma perda de 25% da energia mecânica do sistema, determine a magnitude da força F1 em termos da magnitude de F2.
ITA 2023 - QUESTÃO 03
Considere um recipiente que contém uma coluna de água de altura H. Um pequeno furo é feito na parede a uma altura h, de tal forma que um filete de água é expelido horizontalmente, como na figura.
Considere a água um fluido incompressível e de viscosidade desprezível. A aceleração local da gravidade vale g.
Determine:
a) a trajetória y(x) do filete de água descrito;
b) o lugar geométrico dos pontos P(x, y) que podem ser atingidos por um filete de água, considerando que a altura h possa ser escolhida entre 0 e H.
ITA 2023 - QUESTÃO 04
Considere uma nave espacial esférica, de raio R, com paredes de espessura h ≪ R. No espaço profundo, existe uma radiação cósmica de fundo de temperatura T0 (aproximadamente 2,7 K).
Seja a temperatura da parede interna da nave Ti, e a temperatura da parede externa Te, com Ti > Te > T0. A condutividade térmica do material que compõe a parede da nave é k; o seu calor específico é c e sua densidade de massa é ρ.
A emissividade da nave é unitária e a constante de Stefan-Boltzmann é dada por σ Quando ocorrem pequenas variações de temperatura na parede interna da nave, a condição de fluxo estacionário de calor é perturbada e o sistema tende a uma nova situação de fluxo estacionário de energia.
A constante de tempo característica τ desse processo pode ser estimada apenas em termos das características do material que compõem o revestimento da nave – k, c e ρ – bem como sua espessura h.
Faça o que se pede:
a) obtenha a equação polinomial cuja raiz forneça Te com os coeficientes em termos de k, σ, h, Ti e T0, considerando a condição de fluxo de calor estacionário;
b) estime, por análise dimensional, uma expressão para τ.
ITA 2023 - QUESTÃO 05
Um emissor de onda sonora esférica de frequência fs executa um movimento circular uniforme com velocidade angular ω e raio r em torno da origem O do plano xy, de acordo com a figura.
Ao mesmo tempo, um receptor sonoro executa um movimento no eixo y de forma que sua posição sempre coincida com a coordenada y do emissor. A velocidade do som é designada como vsom.
Sabe-se que o gráfico da frequência da onda sonora detectada no receptor, fob; em função da coordenada x do emissor, aproxima-se de uma cônica para o caso em que ωr ≪ vsom.
Determine:
a) a velocidade máxima alcançada pelo receptor;
b) a cônica e sua equação.
ITA 2023 - QUESTÃO 06
Considere um metamaterial, de índice de refração n1 < 0 e espessura d1, depositado sobre um meio de índice de refração n2 > 0.
Nesse meio, um objeto A dista d2 da interface com o metamaterial, como na figura. Considere pequeno o ângulo que se forma entre o raio óptico que vai do objeto ao observador e a normal da interface entre o metamaterial e o ar.
Nesse caso, vale a aproximação tg θ ≈ sen . Determine n1 em função de n2, d1 e d2 para que a imagem final do objeto se forme na interface entre o ar e o metamaterial.
ITA 2023 - QUESTÃO 07
Uma roda de raio d pode girar livremente com relação ao seu centro O, a partir de t = 0, partindo do repouso. Na roda, são fixadas oito cargas elétricas de magnitude q (q > 0), equiespaçadas, como na parte inferior da figura.
Na região, há um campo elétrico não uniforme no sentido positivo do eixo x. A magnitude desse campo é dada pelo gráfico da parte superior da figura, sendo y = 0 a extremidade inferior da roda, como na parte inferior da figura.
A respeito do movimento, determine:
a) o sentido de rotação da roda imediatamente após o início do movimento, justificando sua resposta;
b) o módulo do torque por causa da força elétrica, em t = 0, relativamente ao centro da roda.
ITA 2023 - QUESTÃO 08
Um laboratório de paredes adiabáticas possui N computadores de alta performance que precisam ser mantidos a uma temperatura T.
Para isso, é instalado um ar-condicionado que atua como uma máquina térmica de máxima eficiência possível, operando entre a temperatura do laboratório e a temperatura do meio externo Te. Cada computador possui nc circuitos.
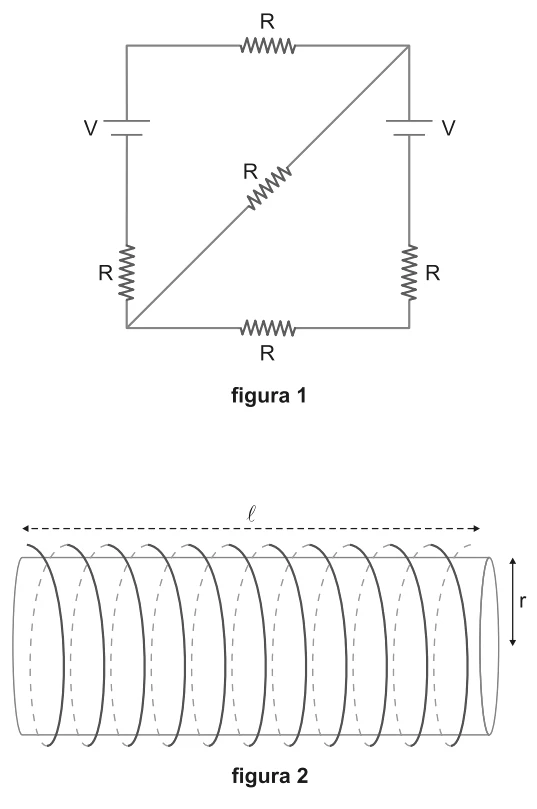
A Figura 1 é o esquema de um circuito. Cada resistor de cada circuito é formado por um fio de cobre de diâmetro ∈, com nv voltas por unidade de comprimento, enrolado em um cilindro de cerâmica de raio r e comprimento l, como na Figura 2.
Determine:
a) a potência dissipada pelos computadores, considerando ρ0 a resistividade do cobre a uma temperatura padrão T0 e α o seu coeficiente de temperatura;
b) a energia consumida pelo ar-condicionado em 1 dia.
ITA 2023 - QUESTÃO 09
Considere duas barras metálicas longas, 1 e 2, dispostas paralelamente uma à outra, em um plano horizontal sem atrito.
Seja L o comprimento das barras; 2r, o diâmetro da seção transversal circular; ρ, a densidade volumétrica de massa; e σ, a condutividade elétrica. A barra 1 está conectada a uma fonte de tensão contínua U1.
A barra 2 é presa em seu centro de massa por uma mola de constante elástica k. Inicialmente, a barra 2 está conectada a uma fonte de corrente I2 e encontra-se em equilíbrio estático a uma distância d da barra 1.
No instante t1, a fonte de corrente é desconectada da barra 2, a qual passa a mover-se livremente no plano.
Calcule a velocidade máxima adquirida pela barra 2.
ITA 2023 - QUESTÃO 10
Feixes de luz de comprimentos de onda 590 nm, 450 nm e 380 nm incidem sobre uma superfície metálica. Com um aparato experimental, são medidas as velocidades dos fotoelétrons ejetados. Sabendo que a maior velocidade detectada foi de 640 km/s. faça o que se pede:
a) determine a função trabalho do material;
b) determine a frequência de corte:
c) justifique se é possível que um elétron livre absorva um fóton, tal como ocorre no efeito fotoelétrico em um material. Um elétron livre é um elétron sem interações com outros corpos, além do referido fóton.















COMENTÁRIOS